Mixed CostDefinition, Formula, and How to Calculate

In running a business, you’ll be encountering costs that differ in behavior.

Some costs go up or down depending on the level of sales or production.

These costs are what we refer to as variable costs.

For example, the commission you pay your sales employees for every sale made goes up as sales increase.

Likewise, if sales decrease, the commission expense will also decrease.

Then there are costs that stay the same no matter the level of activity.

They’re what we call fixed costs.

Fixed cost will relatively stay the same whether you make a sale or not.

For example, you will have to pay the rent for the office space you’re using whether you make a sale or not.

Even if you made a sale of $500 or $5,000, the rent that you’ll be paying will still be the same.

Finally, there are costs that behave the same as variable and fixed costs.

What I mean to say is that these costs vary depending on the level of activity, but they also have a portion that stays as-is.

These costs are what we refer to as mixed costs.

For example, let’s say that you subscribe to a water refilling service that will charge you $400 for the first 1,000 gallons, and $1 for every gallon thereafter.

This makes the cost of water a mixed cost as it has variable and fixed components.

The $400 is the fixed component as you’ll be paying for it no matter how many gallons of water you consume.

The $1 per gallon on the other hand is the variable component as you’d only incur it if you consume more than 1,000 gallons of water.

If you only consume 1,000 or less gallons of water, you’d only be paying the fixed portion which is $400.

What is a mixed cost?

A mixed cost is a cost that has both the characteristics of variable and fixed costs.

Meaning that it has a component that increases or decreases with the level of activity.

It also has a component that stays as-is no matter what the level of activity is.

Mixed cost is also referred to as semi-variable or semi-fixed cost.

A typical manufacturing process will include fixed and variable costs.

As such, you could say that the total manufacturing cost is a mixed cost.

That’s not to say that there aren’t individual costs that are mixed costs though.

Because there are.

For example, you subscribed to a phone plan that charges you $50 for the first 10GB of mobile data.

It then charges you $7 for every 1GB thereafter.

This makes the phone plan a mixed cost as it has both fixed and variable components.

The $50 you pay is a fixed component as you’ll have to pay it whatever amount of data you consume.

The $7 for every 1GB of mobile data is a variable component as you’d only incur it if you exceed 10GB mobile data consumption.

If you consume only 5GB of data, you’d still be paying $50.

Whereas, if you consume 15GB of data, you’ll be paying $50, and on top of that, $35 for the 5GB over the first 10GB, which amounts to a total of $85.

It’s important for any business to know the cost behavior of the expenses that they incur.

Doing so will prepare them for the differing total costs for every level of activity.

It also helps in budgeting for future accounting periods.

If a business knows the cost behavior of the costs it incurs, it can predict (to a certain extent) the total amount of costs it will incur.

The mixed cost formula

To easier compute for you mixed costs, you can use a certain formula:

Mixed Cost = a +bx

Where:

a = the fixed component of the mixed cost

b = the variable component of the mixed cost (per unit)

x = the level of activity in units

Let’s go back to the phone plan example we had above.

We already established that the $50 is the fixed component, will be our variable a.

The $7 per 1GB of data consumption is the variable component, which will be our variable b.

Our variable x will be the amount of data consumption (in units) in excess of the first 10GB.

Let’s say that for the past month, you consumed a total of 20GB of mobile data.

To know your total phone plan cost, we will use the mixed cost formula:

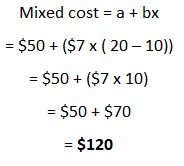
If your mobile data consumption didn’t exceed 10GB, then you won’t have to use the formula.

The total cost of the phone plan would be equal to the fixed component of $50.

This is because the level of activity hasn’t reached a point where you have to incur a variable cost.

Segregating the fixed and variable components of a mixed cost

In the preparation of budgets, it is important to segregate the fixed and variable components of a mixed cost.

This is because the two components don’t behave in the same way.

The fixed component will relatively stay the same whatever the level of activity is.

On the other hand, the variable component will go up or down depending on the level of activity.

Budgeting a mixed cost without segregating these two components might result in a faulty budget.

You might consider the mixed cost as a wholly fixed or variable cost.

Fortunately, there are many known methods that can be used to segregate the fixed and variable components of a mixed cost.

Some of these are the following:

High-low Method

The high-low method is probably the simplest and easiest method of segregating the fixed and variable components of a mixed cost.

It only needs two data values from a set of data: the highest and lowest values.

It can even be used with a limited set of data.

Also, it doesn’t need a complex accounting software as you can use it even with a simple calculator.

The high-low method actually uses two formulas: one for the variable component, and the other for the fixed component.

The formula for the computation of the variable component is as follows:

Variable Component Per Unit = (HAC – LAC) ÷  (HAU – LAU)

Where:

HAC = Highest activity cost or the cost at the highest level of activity

LAC = Lowest activity cost or the cost at the lowest level of activity

HAU = Highest activity units or the number of units at the highest level of activity

LAU = Lowest activity units or the number of units at the highest level of activity

Whereas, the formula for the computation of the fixed component has two variants:

 

Fixed Component = HAC – HAVC

Where:

HAC = Highest activity cost or the cost at the highest level of activity

HAVC = Highest activity variable component or the total variable component at the highest level of activity; it can be computed by multiplying the highest activity units with the variable component per unit

 -or-

 

Fixed Component = LAC – LAVC

LAC = Lowest activity cost or the cost at the lowest level of activity

LAVC = Lowest activity variable component or the total variable component at the lowest level of activity; it can be computed by multiplying the lowest activity units with the variable component per unit

Least Squares Method (Linear Regression)

The least squares method (linear regression) is probably the most accurate method of segregating the fixed and variable components of a mixed cost.

It uses a series of computations to arrive at the variable cost per unit, as well as the total fixed cost.

It requires knowledge of algebra and statistics though, making it the most demanding method of segregating the fixed and variable components of a mixed cost.

The least squares method is based on the linear equation:

y = a +bx

Where:

y = mixed cost

a = fixed component of the mixed cost

b = variable component of the mixed cost (per unit)

x = level of activity (in units)

To get the variable component of the mixed cost, the following formula is used:

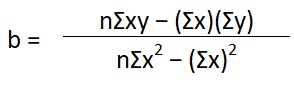
Where:

b = variable component per unit

n = number of data pairs (cost and units) used in the calculations

x = total units per data pair

y = total cost per data pair

xy = total units multiplied by total cost per data pair

To get the fixed component of the mixed cost, the following formula is used:

Where:

a = total fixed component

b = variable component per unit

n = number of data pairs (cost and units) used in the calculations

x = total units per data pair

y = total cost per data pair

Scatter Graph Method

Unlike the previous two methods that solely rely on mathematical formulas, the scatter graph method uses a graph.

Specifically, a scatter graph (hence the name).

Under this method, a set of data is plotted on a graph.

The X-axis will represent the total units for each activity level, while the Y-axis will represent the mixed cost.

Much like the least squares method, the scatter graph method considers all data values in a set of data.

This makes it a level higher than the high-low method which only takes the two extreme values (highest and lowest) into account.

Furthermore, the scatter graph method also uses the linear equation “y = a + bx” in the computation of mixed cost.

The point where the pair of values (unit and cost) meet is where we plot a data point.

Do this for every data point and you’ll have a scatter graph.

When all data points are plotted, we then draw a trendline.

The point where the trendline touches the Y-axis represents the fixed component of the mixed cost.

The slope of the trendline indicates the degree of the variable component.

The steeper it is, the higher the variable component per unit is.

Once the fixed component is determined/estimated, the variable component can then be computed using the formula:

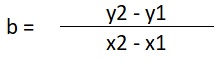Where:

b = variable component per unit

y = total cost

x = total units

For variables x and y, you can use any two data points from the trendline.

The most glaring limitation of the scatter graph method is that the trend line is essentially an estimate.

That means that the resulting equation may not be 100% accurate due to the estimation.

But since it uses more data points than the high-low method, it tends to be more reliable.