Modified DurationThe sensitivity of the value of a security to changes in interest rates
At a glance, one may think that it’s easier to understand bonds than stocks.
The face value is the principal amount that you’ll receive at the maturity of the bonds.
The coupon rate is the amount of interest you’ll periodically receive during the life of the bond.
For example, let’s say that a bond has a face value of $1,000 with a 3-year duration and an annual coupon rate of 6.5%.
This means that the bondholder will receive $1,000 at the maturity of the bond.
On top of that, s/he should expect to receive $65 ($1,000 x 6.5%) annually during the duration of the bond. Pretty easy to understand, right?
Turns out bonds are more complex than stocks.
While yes, understanding a bond’s face value, its duration, and its coupon rate (or interest rate) is easy, other things about a bond can be much more complex.
Particularly, determining the value of a bond requires fairly complex calculations.
Investors need to be savvy regarding the valuation of bonds as they are more sensitive to changes in interest rates compared to stocks.
One of the tools of bond valuation is referred to as the “modified duration”.
In this article, we will explore what modified duration is.
How does one calculate modified duration?
What does modified duration tell us?
How does it help with bond valuation?
We will try to answer these questions as we go along with the article.
We will also have some examples so that we can further understand the calculation of modified duration.
What is Modified Duration?
Modified duration is a formula that conveys the measurable effect of a change in interest rates on the price/value of a security.
It’s commonly used in bond valuations. It follows the concept that bond prices and interest rates move inversely to each other.
For example, if interest rates go up, bond prices go down. If interest rates go down, bond prices go up.
Modified duration presents a measurable change in bond prices due to changes in interest rates.
Particularly, it presents the effect that a 100-basis-point (1%) change in interest rates will have on the price of a bond or security.
So if the modified duration shows a figure of 2.21, it means that the price of the bond will increase or decrease by 2.21% for every 1% change in interest rates.
To further understand modified duration, let’s take a look at the formula for its calculation:
Modified Duration = Macaulay Duration ÷ ( 1 + (YTM ÷ n))
Where:
Macaulay Duration – this refers to the weighted average number of years it will take for a bondholder to recover the money s/she initially invested in the bond. It is the point where the present value of the bond’s cash flows becomes equal to the amount paid for the bond
YTM – an acronym for Yield to Maturity, refers to the return a bond would yield if it is held until maturity
n – refers to the number of coupon periods per year. For example, if n is 1, it means that the bond pays interest annually. If n is 2, it means the bond pays interest twice every year, usually semi-annually.
As we can see from the formula, there is a component called the Macaulay duration.
This means that before we can calculate the modified duration, we first have to calculate the Macaulay duration.
So what is it?
What is the Macaulay Duration?
The Macaulay duration is a figure that represents the weighted average of time it would take until the present value of cash flows equal the amount paid for the bond or security.
In other words, it’s the amount of time a bondholder requires to recover his/her initial investment in a bond.
It is often expressed in years, so if the Macaulay duration states 4.51, it means that the bondholder has to hold on to the bond for at least 4.51 years for him/her to recover his/her initial investment.
Typically, the higher the Macaulay duration, the more sensitive the bond’s price will be to changes in interest rates.
We can tell this from the modified duration formula wherein the Macaulay duration is a numerator.
Speaking of formulas, let’s take a look at the one we use to calculate the Macaulay duration:
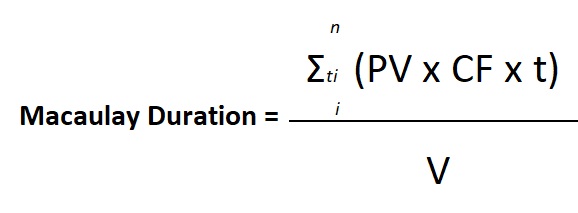
Where:
PV x CF – refers to the present value of cash flows at period t
t – refers to the time to each cash flow in years
n – refers to the number of coupon periods per year
V – refers to the present value of all cash flows; it can also refer to the market price of the bond
Looks complicated, right?
To make it easier to understand, just think of the entire numerator as the summation of all (PV x CF x t) or the present value of each cash flow multiplied by the number of years it takes to receive them.
Still complicated? Let’s lay it out in table form:
Suppose that a 4-year $1,000 bond has an annual coupon rate of 6%.
The prevailing interest rate is 4%.
Here’s what the Macaulay duration would look like if laid out in table form:

Now that we have our numerator and denominator, we can calculate the Macaulay duration of the bond:
Macaulay Duration = $3,953.03 ÷ $1,072.60
= 3.69
As per computation, it will take approximately 3.69 years for the bondholder to recover his/her initial investment on the bond.
Examples of Calculating Modified Duration
Example#1
For our first example, let’s calculate the modified duration of our Macaulay duration example above.
To summarize, the bond has a face value of $1,000, a maturity period of 4 years, and an annual coupon rate of 6%.
The interest rate is 4%. This resulted in a Macaulay duration of 3.69.
In this case, our YTM is 4%, which is the interest rate. Let’s calculate the modified duration:
Modified Duration = Macaulay Duration ÷ ( 1 + (YTM ÷ n))
= 3.69 ÷ (1 + (4% ÷ 1))
= 3.55
As per computation, the modified duration is 3.55.
This means that the price of the bond will increase by 3.55% for every 1% decrease in the interest rate.
On other hand, the price of the bond will decrease by 3.55% for every 1% increase in the interest rate.
Example#2
Let’s say that a 3-year annual payment bond of $3,000 has a Macaulay duration of 2.73 years.
Its YTM is 7.5%. Calculate the modified duration of the bond:
Modified Duration = Macaulay Duration ÷ ( 1 + (YTM ÷ n))
= 2.73 ÷ (1 + (7.5% ÷ 1))
= 2.54
As per computation, the modified duration is 2.54.
This means that the price of the bond will increase by 2.54% for every 1% decrease in the interest rate.
On other hand, the price of the bond will decrease by 2.54% for every 1% increase in the interest rate
FundsNet requires Contributors, Writers and Authors to use Primary Sources to source and cite their work. These Sources include White Papers, Government Information & Data, Original Reporting and Interviews from Industry Experts. Reputable Publishers are also sourced and cited where appropriate. Learn more about the standards we follow in producing Accurate, Unbiased and Researched Content in our editorial policy.
The Coastal Business Journal "Estimating Modified Duration and Convexity for Income Properties " White paper. September 21, 2022
